Correction DS

Correction DS

Exercice 1 : Transformations basiques

On considère le signal représenté ci-dessous :

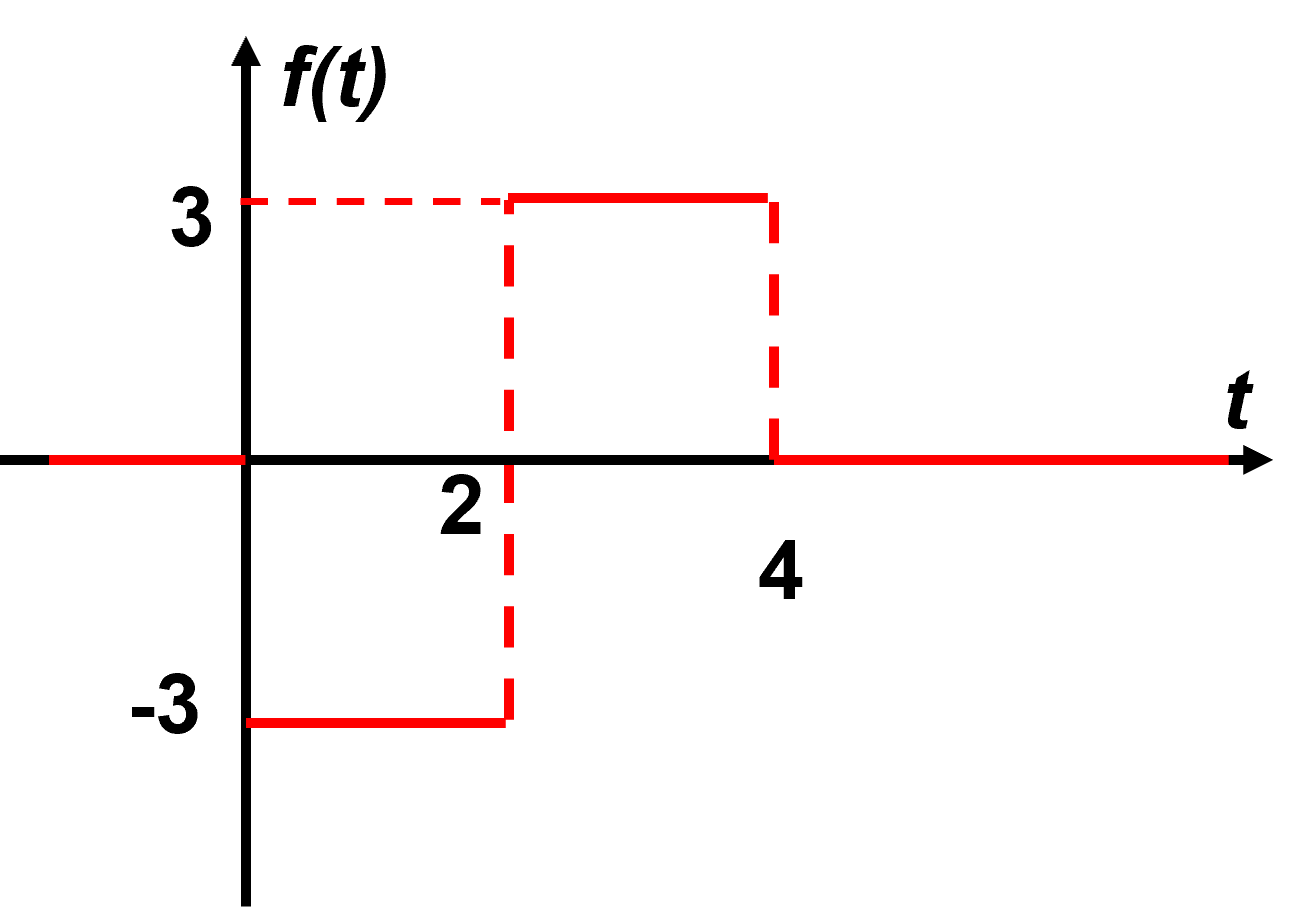
Exprimer la fonction en fonction de la fonction échelon unité U(t).

$f(t) = -3 \left ( U(t)-U(t-2) \right ) \ + 3 \left ( U(t-2)-U(t-4) \right )$

$\boxed {f(t) = -3 U(t) + 3 U(t-2) \ + 3 U(t-2) - 3U(t-4)} $

A l'aide de cette expression et du formulaire, déterminer sa transformée de Laplace.

$F(p) = \dfrac {-3}{p} + \dfrac {3e^{ \ -2p}}{p} + \dfrac {3e^{ \ -2p}}{p} - \dfrac {3e^{ \ -4p}}{p}$

$\boxed {F(p) = \dfrac {-3 + 6e^{ \ -2p} -3e^{ \ -4p}}{p}}$

Exercice 2

On considère le signal défini pour $ t \geq 0 $par : $ f(t) = U(t)-U(t-4) + \left ( t-5 \right )\left ( U(t-6) - U(t-4) \right ) $

1. Représenter le signal dans un repère orthonormé.

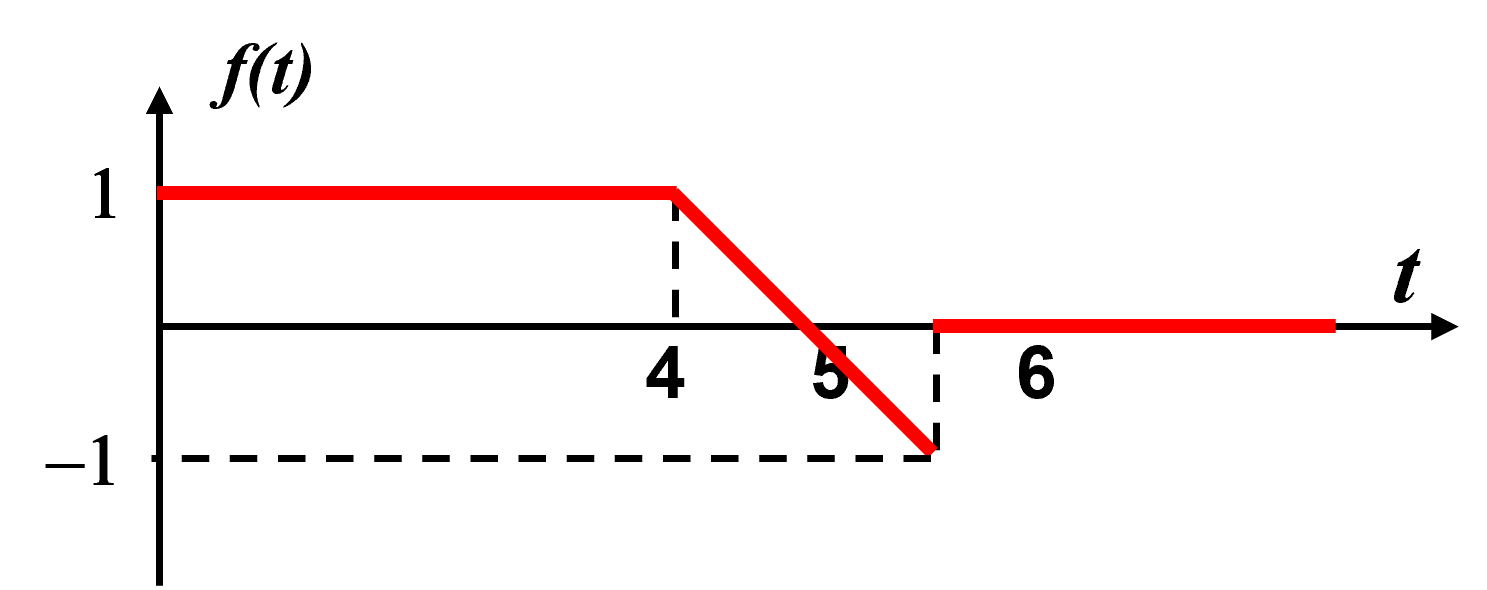
2. Déterminer sa transformée de Laplace.

$ f(t) = U(t)-U(t-4) + \left ( t-5 \right )\left ( U(t-6) - U(t-4) \right ) \\ f(t)=U(t)-U(t-4) + ( t-5-1+1 ) ( U(t-6) - U(t-4) ) \\ \boxed{f(t)=U(t)-U(t-4) + (t-6 ) U(t-6) + U(t-6) - (t-4)U(t-4) +U(t-4)} \\ F(p) = \dfrac{1}{p} - \dfrac{e^{-4p}}{p} + \dfrac {e^{ \ -6p}}{p^{ \ 2}} + \dfrac {e^{ \ -6p}}{p} - \dfrac {e^{ \ -4p}}{p^{ \ 2}} + \dfrac {e^{ \ -4p}}{p} \\ \boxed{F(p) = \dfrac{1}{p} + \dfrac {e^{ \ -6p}}{p^{ \ 2}} + \dfrac {e^{ \ -6p}}{p} - \dfrac {e^{ \ -4p}}{p^{ \ 2}}}$

Exercice 2 : Transformées de Laplace

Déterminer la transformée de Laplace des signaux proposés:

1) $x(t) = e^{ \ -2t}U(t)$	2) $z(t) = sin(2t)U(t)$
$\boxed{X(p)=\dfrac{1}{p+2}}$	$\boxed{ Z(p) = \dfrac { 2}{p^{ \ 2}+4}}$

Exercice 3 : Transformée de Laplace inverse.

1. Déterminer le signal original à la réponse ci-dessous :

$Y(p)=\dfrac{p+5}{p^{ \ 2}+2p+4}$

Le dénominateur $p^2+2p+4$ n'a pas de racine réelle $\left ( \Delta \ = 2^2 \ - \ 4 \times 1 \times 4 \ = \ -12 \ < \ 0 \right )$, il faut l'écrire sous sa forme canonique.

$p^2 \ + \ 2p \ + \ 4 \ = \ \left ( p \ + \ 1 \right ) ^2 \ + \ 3 $

$Y(p)=\dfrac{p+5}{p^{ \ 2}+2p+4} = \dfrac{p+5}{(p+1)^2+3} $

Dès lors, au dénominateur, un décalage dans le plan de Laplace apparaît : $p \ + \ 1$

Il faut le faire appararaître au numérateur pour pouvoir l'appliquer : $p \ + \ 5 \ = \ p \ + \ 1 \ + \ 4$

Alors :

$Y(p)=\dfrac{p+5}{p^{ \ 2}+2p+4} = \dfrac{p +1 }{(p+1)^2+3} + \dfrac{4}{(p+1)^2+3}$

$ Y(p)= \dfrac{p+5}{(p+1)^2+3} = \dfrac{p+1}{(p+1)^2+(\sqrt{3})^2 } + \dfrac{4}{\sqrt{3}}\times \dfrac{\sqrt{3}}{(p+1)^2+(\sqrt{3})^2}$

Et donc :

$\boxed{ y(t) = e^{ \ -t} \times cos (\sqrt{3}t) + \dfrac{4e^{ \ -t}}{\sqrt{3}} \times sin(\sqrt{3}t)}$

2. Déterminer le signal original à la réponse ci-dessous :

$Y(p)=\dfrac{p}{p^{ \ 2}+8}$

$\boxed{z(t) = cos(2 \sqrt{2}t)} $