Les Cristaux

ACTIVITES

A1 : L'organisation de la matière dans les solides.

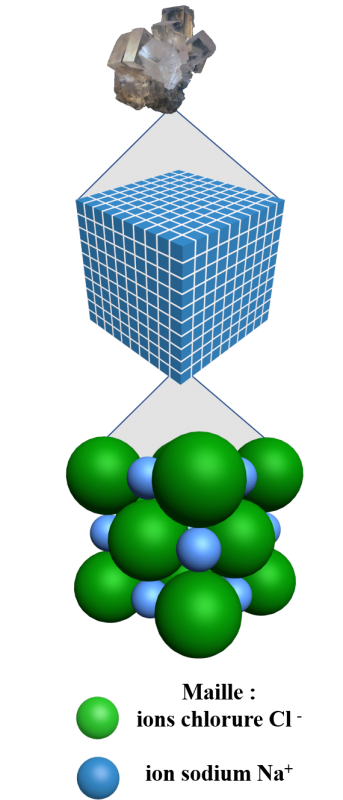
A11. Les cristaux de sel.

Doc 1.

Les marais salants sont des exploitations permettant la production du sel. Ils sont constitués de bassins de grande surface et de faible profondeur alimentés en eau de mer. L'eau s'évapore sous l'action du Soleil et du vent, et c'est ainsi que l'on obtient la cristallisation du sel dissout dans l'eau de mer. Le sel, alors à l'état solide, s'accumule par décantation au fond des bassins, où il peut ensuite être récolté par les sauniers.

Doc 2.

L'abbé René-Just Haüy (1734-1822), minéralogiste français, est l'un des fondateurs de la cristallographie moderne (étude géométrique des cristaux). C'est en 1781, alors qu'il examine un cristal de calcite, que celui-ci lui échappe des mains et se brise sur le sol. Il observe alors que les fragments résultants ont conservé la même forme géométrique que le cristal de départ, et ce, indépendamment de leur taille. Il émet ainsi l'hypothèse de l'existence de "molécules intégrantes" qui, empilées les unes aux autres, génèrent le cristal.

En 1913, William Henry Bragg (1862-1942), chimiste britannique, décrit la nature cristalline du chlorure de sodium NaCl, composant majoritaire du sel de cuisine. Il démontre que les ions chlorure (Cl-) et les ions sodium (Na+) s'emplilent de façon régulière comme l'avait prédit René-Just Haüy presque deux siècles plus tôt. Cette organisation microscopique caractérise un solide cristallin, appelé "cristal".

Le chlorure de sodium est décrit au niveau microscopique par une maille de forma cubique, reflet de l'arrangement des ions qui le constituent. L'empilement régulier et périodique des mailles génère le cristal de chlorure de sodium à l'échelle macroscopique. C'est ce que l'on appelle l'état cristallin.

? Nommer le changement d'état physique observé par l'eau dans le bassin d'un marais salant.

? Comment est qualifiée l'organisation de la matière dans le sel (chlorure de sodium) ?

? Comment se nomme le motif élémentaire observé dans le sel ?

? Justifier que le sel soit un solide cristallin.

? A quoi se réfèrent les "molécules" intégrantes supposées par l'abbé Haüy ?

? A partir du document 2, identifier les étapes relevant de la démarche scientifique. Pourquoi les découvertes peuvent mettre plusieurs siècles à être confirmées.

A12. Le verre.

*Doc 3.* Les premiers objets en verre datent d'environ 2500 ans avant J.C. et ont été retrouvés en Egypte et au Proche-Orient. A l'aide de l'extrémité de son tube en acier, appelé "canne du verrier", le souffleur de verre recueille la pâte de verre en fusion à environ 1300°C. En soufflant dans la canne, l'artisan lui donne la forme désirée.
	Le verre n'est pas un solide cristallin car les atomes qui le constituent sont disposés de façon totalement aléatoire : c'est un solide amorphe. L'analyse microscopique de la silice (SiO2), principal constituant du verre montre que les atomes de silicium et d'oxygène ne suivent pas un arrangemant ordonné.

? Qu'est-ce qui différencie un solide cristallin d'un solide amorphe ?

A2 : Le cristal d'argent.

L'argent est un métal précieux, utilisé en joaillerie ou en orfèvrerie. Il est facilement malléable, ce qui permet de lui faire prendre la forme désirée.

Question : Comment est organisé microscopiquement l'argent solide ?

Doc 1 : Description du système cubique.

? Un système peut cristalliser sous différentes formes géométriques, comme le cube.

Dans ce cas particulier, les atomes sont placés aux sommets d'un cube. Ils sont représentés par des sphères tangentes les unes aux autres.

? Aux sommets de la maille, les entités sont partagées entre huit mailles élémentaires voisines. Seul un huitième (1/8) de cette entité est contenu dans une maille.

Le cube ayant huit sommets, la maille contient au total :

$ 8\times \dfrac {1}{8} = \color{blue} {1 \ entité} $

? La compacité permet de comparer le volume occupé par les entités contenues dans la maille et le volume de la maille.

Les entités étant représentées comme des sphères tangentes les unes aux autres, la compacité est définie par :

$ C = \frac {Volume \ occupé \ par \ les \ entités}{Volume \ de \ la \ maille }$

$ \color{red}{R} = \dfrac {\color{#00ff00}{a}}{2}$

$$ \color{red}{C}= \dfrac {\color{blue}{1}\times \dfrac {4\pi \color{red}{R}^3}{3}}{\color{#00ff00}a^3}=
\dfrac {\dfrac {4\pi}{3}\left ( \dfrac {\color{#00ff00}{a}}{2} \right ) ^3}{\color{#00ff00}a^3 }=
\dfrac {\dfrac {4\pi}{24}\color{#00ff00}a^3}{\color{#00ff00}a^3} \color{red} {= \dfrac {\pi }{6} = 0,52}
$$

Doc2 : Masse d'une maille.

En connaissant le nombre d'entités présentes dans la maille, on peut déterminer sa masse.

$ M_{maille} = \dfrac {N \times M}{\mathcal {N}_a} $

N : nombre d'entités dans la maille

M : masse molaire (g.mol^-1)

N_a : constante d'Avogadro N_a = 6,02.10²³

Doc3 : Données sur l'argent

L'argent cristallise dans un système cubique dont les caractéristiques sont :

Paramètre de la maille : a = 4,08 Å

Masse volumique :$\rho = 10,5 \ g.cm^{-3}$

Masse molaire : M(Ag) = 107,87 g.mol^-1.

Rappel : 1 Å = 10^-10 m.

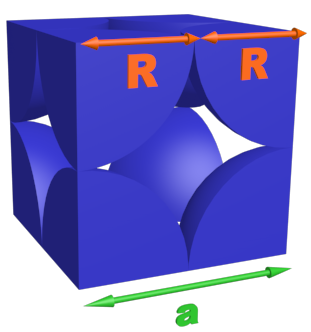
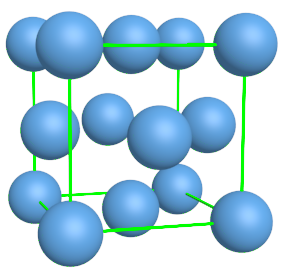
Doc 4 : Le système cubique à faces centrées.

Les entités sont organisées aux sommets d'un cube et aux centres de chaque face.

Elles sont en contact selon la diagonale de chaque face.

vues en 3D

? Déterminer le nombre d'entités par maille dans le système cubique à faces centrées.

? Dans le système cubique à faces centrées, déterminer l'expression de R en fonction de a.

? Dans le système cubique à faces centrées, déterminer la compacité C.

? Comparer cette compacité à celle du système cubique simple.

? Quel est le système le plus compact ?

? Ce résultat est-il en accord avec l'organisation des atomes dans la maille ?

? Rappeler la formule littérale donnant la masse volumique ρ , la masse m et le volume V.

? Pour chaque système, donner l'expression de la masse volumique ρ en fonction du paramètre a et du nombre d'entités N.

? En déduire le système cristallin de l'argent.

COURS

C1. L'état solide.

C11. Définition de l'état solide.

C'est l'état condensé de la matière obtenu par solidification d'un liquide par condensation d'un gaz .

C12. Entité chimique.

Une entité chimique désigne des espèces toutes identiques les unes aux autres (atomes, ions, molécules).

C13. Solide amorphe, cristal.

Un solide cristallin d'un assemblage périodique régulier d'entités (atomes, ions, molécules).

Dans un solide amorphe l'assemblage est désordonné.

C2. Solide cristallin.

C21. Définition.

C'est un assemblage périodique régulier d'entités. Il existe des solides ioniques composé d'ions comme le chlorure de sodium solide, les solides covalents composé d'atomes et les solides moléculaires composé de molécules.

C22. Maille élémentaire.

C'est le plus petit motif de l'organisation des entités qui se répète dans le solide.

C3. Systèmes cubiques.

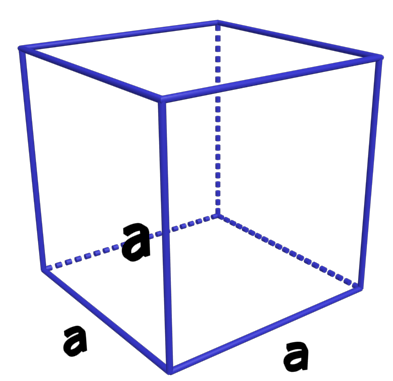
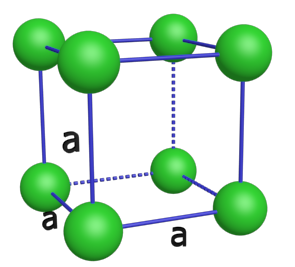
C31. Cubique simple.

Les entités sont organisées aux sommets d'un cube.

A chaque sommet, 1/8 de l'entité est dans la maille.

Au total, il y a : $ 8 \times \dfrac {1}{8} $ entité dans la maille.

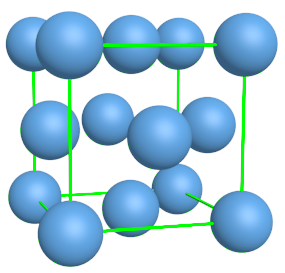
C32. Cubique à faces centrées.

Les entités sont organisées aux sommets d'un cube et aux centres de chacune des faces.

A chaque sommet, il y a 1/8 de l'entité présente dans la maille.

Au centre de chaque face, il y a 1/2 de l'entité présente dans la maille.

Au total, il y a : $8\times \dfrac {1}{8} + 6 \times \dfrac {1}{2} = 4 $ entités présentes dans la maille.

C33. Compacité.

C33a. Définition.

La compacité définit le taux d'occupation des entités dans la maille.

C'est le rapport du volume occupé par les entités présentes dans la maille au volume de la maille.

$ C = \dfrac {Volume \ occupé \ par \ les \ entités}{Volume \ de \ la \ maille }$

C33b. Comparaison des deux systèmes.

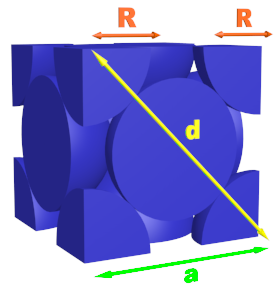
Système cubique simple :

Les atomes sont en contact le long de l'arête.

On a donc : $ a=2R \ soit \ R= \dfrac {a}{2} $

$ C_{cubique} =\dfrac { 1\times \dfrac {4}{3} \pi R^3}{a^3}$
$ C_{cubique} =\dfrac { 1\times \dfrac {4}{3} \pi \left ( \dfrac {a}{2} \right )^3}{a^3}$
$C_{cubique} = \dfrac {\pi}{6} = 0,52 $

Système cubique à faces centrées :

Les atomes sont en contact le long de la diagonale d'une face.

On a donc : $ 4R =a \sqrt 2 \ soit \ R= \dfrac {a\sqrt 2}{4} $

$C_{cfc} =\dfrac { 4\times \frac {4}{3} \pi R^3}{a^3}$
$C_{cfc} =\dfrac { 4\times \dfrac {4}{3} \pi \left ( \dfrac {a\sqrt 2}{4} \right )^3}{a^3}$
$C_{cfc} = \dfrac {\pi \sqrt 2}{6} = 0,74 $

Le système cubique à faces centrées et donc plus compact que le système cubique.

C4. Du microscopique au macroscpiques.

La structure microscopique d'un cristal conditionne certaines de ses propriétés macroscopiques, comme la masse volumique ρ.

· Au niveau macroscopique, cette dernière s'exprime comme le rapport d'une masse du solide au volume occupé par cette masse :

$\rho = \dfrac {m}{V} $

m : masse exprimée en grammes (g)

V : volume exprimé en cm³.

ρ: masse volumique exprimée en g/cm³

· Au niveau du microscopique, elle correspond donc au rapport de la masse d'entités présentes dans la maille au volume de cette maille :

$\rho = \dfrac {m_{maille}}{V_{maille}} $

La masse de la maille est : $ M_{maille} = \dfrac {N \times M}{\mathcal{N}_a}$

N : nombre d'entités dans la maille

M : masse molaire exprimé en g.mol^-1

N_a : nombre d'Avogadro.

· Dans un système cubique d'arête a (exprimée en cm), la masse volumique est donc :

$\rho = \dfrac {N \times M}{a^3 \times \mathcal{N}_a} $

Exercices : de la page 36 à 42.

Numéros : 4 ; 6 ; 7 et 10

Commentaires

- 1. vvghjl Le 25/11/2021
Coucou ! Pour ceux qui viennent demander le corriger par la suite, sachez que vous ne l'aurai pas ;)
Demander de l'aide mais le but est de progresser et non de recopier bêtement.
Bonne journée et belle vie à vous !
- 2. Ghomérani Jamel Le 07/11/2021
Bonjour,
Serait-il possible d'avoir le corrigé de cet exercice par mail, svp? Merci d'avance.

Cordialement
- 3. Mat Le 13/11/2020
Bonjour j’ai beaucoup de mal avec cette activité es ce que vous pourriez m’envoyer le corriger par mail svp
Merci d’avance
- 4. Maxime Le 12/11/2020
Bonjour,
Serait-il possible d’avoir le corrigé des question sur les cristaux de sel par mail svp car je ne comprends pas tout.
Cordialement.
- 5. charles ana Le 31/10/2020
bonjours j'aimerait sil vous plait voir de laide avec les premier exercice cas je n'y arrive pas
- 6. lili Le 03/10/2020
bonjour
Pouvez vous l'envoyer le corriger par mail svp je n'ai tout bien compris
- 7. Grégory Serclier-Pieri Le 22/06/2020
Bonjour.
Je veux bien vous aider, mais je n'envoie pas corrigé.
- 8. Julie Le 26/01/2020
Pourriez vous m’enoyer les corrigés par mail svp je comprends pas bien
- 9. Herledant Le 15/12/2019
Bonjour pourrais je avoir le corriger de ce document s’il vous plaît ?
- 10. marie Le 15/12/2019
pourriez-vous m'envoyer le corrigé svp car contrôle type bac demain
- 11. Coyote Le 21/11/2019
Par contre, bientôt, je compléterai avec le cours.
- 12. Coyote Le 21/11/2019
Bonjour à tous.
Je ne peux pas répondre directement à toutes les questions, ni vous donner un corrigé.
Par contre, je peux répondre à des questions bien précises pour vous aider à y répondre et progresser dans votre démarche.
Cordialement.
- 13. Xi Le 13/11/2019
- 14. Mariiiie Le 10/11/2019
Bonjour, je voudrais également avoir les corrigés des questions, serait-il possible de me les envoyer ?
- 15. BLASCO Le 07/11/2019
bonjour
Pourriez-vous m'envoyer le corrige de cet exercice que je puisse aider mon beau-fils dans un genre de problème similaire.

Cordialement
- 16. Isnard Le 02/11/2019
Bonjour je souhaiterais avoir le corrigé de ce document, serait t'il possible de me l'envoyer par mail ? Merci d'avance
- 17. Penso Le 01/11/2019
Au final quel est le système de l’argent svp?
- 18. Nissaï ABDOULATUF Le 23/10/2019
Bonjour est ce que je pourrait avoir de l'aide sur cette sujet merci beaucoup.
- 19. Faida Le 21/10/2019
Merci

Ajouter un commentaire

Nom

E-mail

Site Internet

Message

Aperçu

Anti-spam