Description d'un mouvement
ACTIVITES
A0 : Tracés des vecteurs vitesse et accélération :
A01 : Tracé du vecteur vitesse:
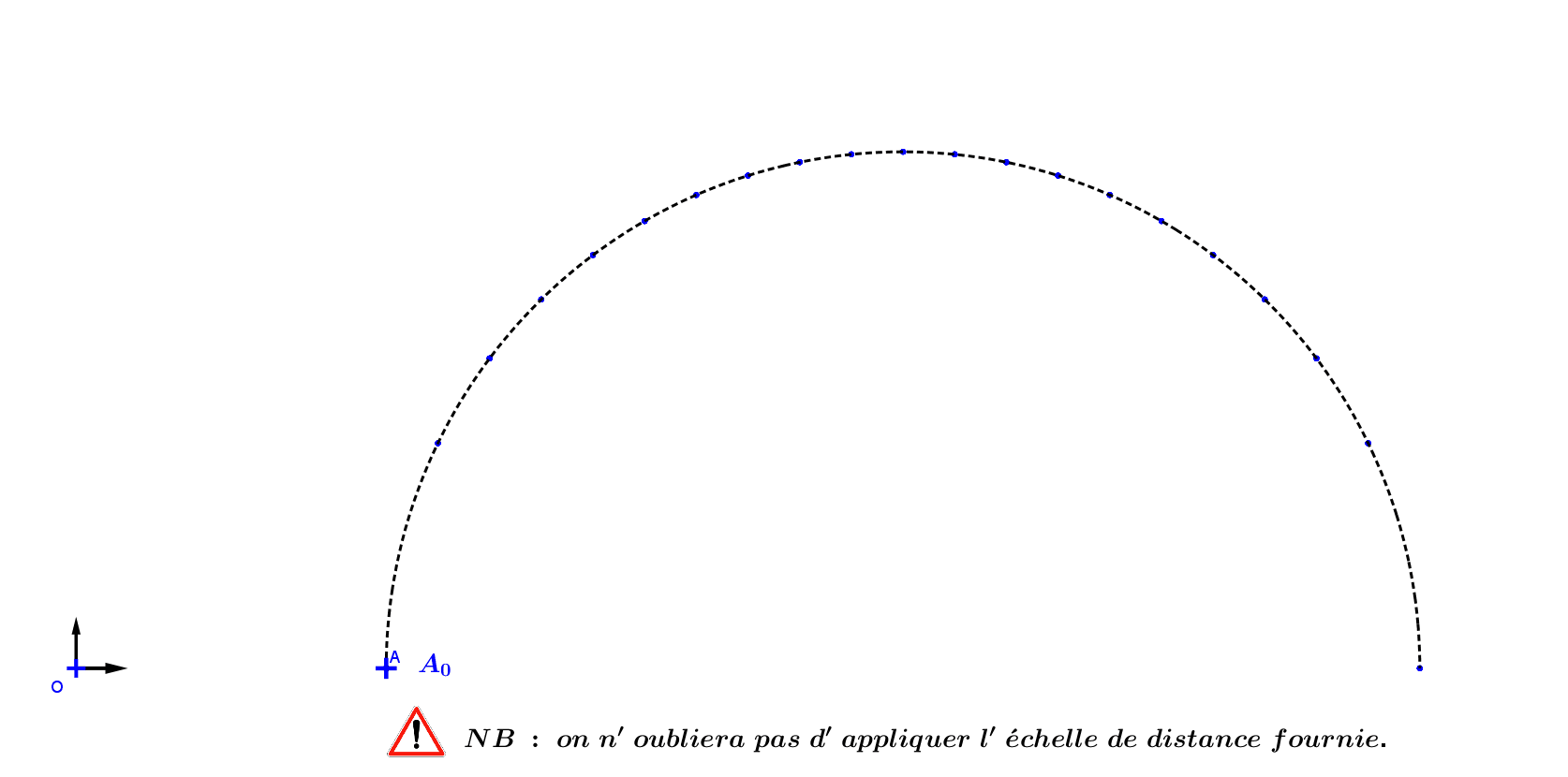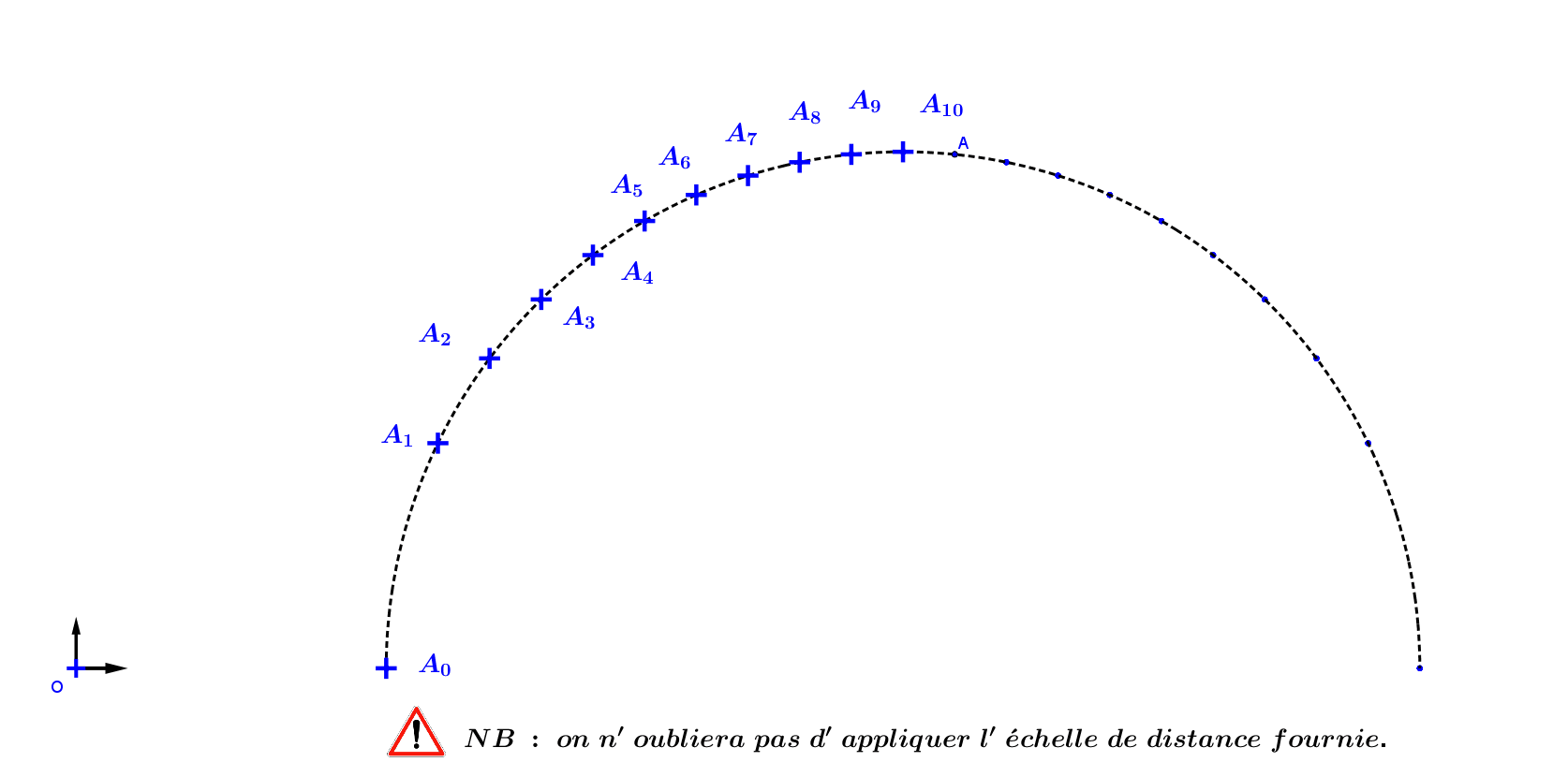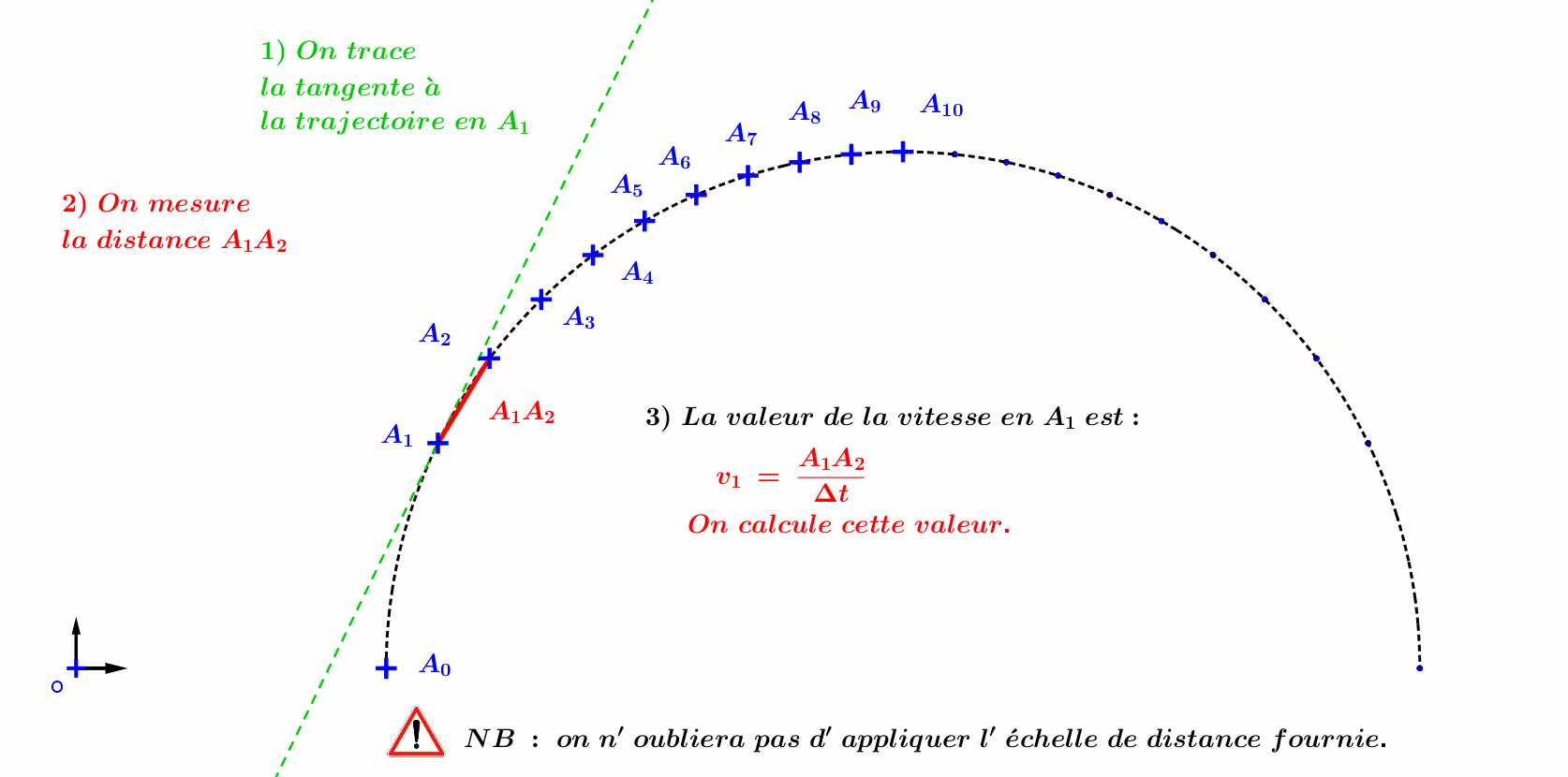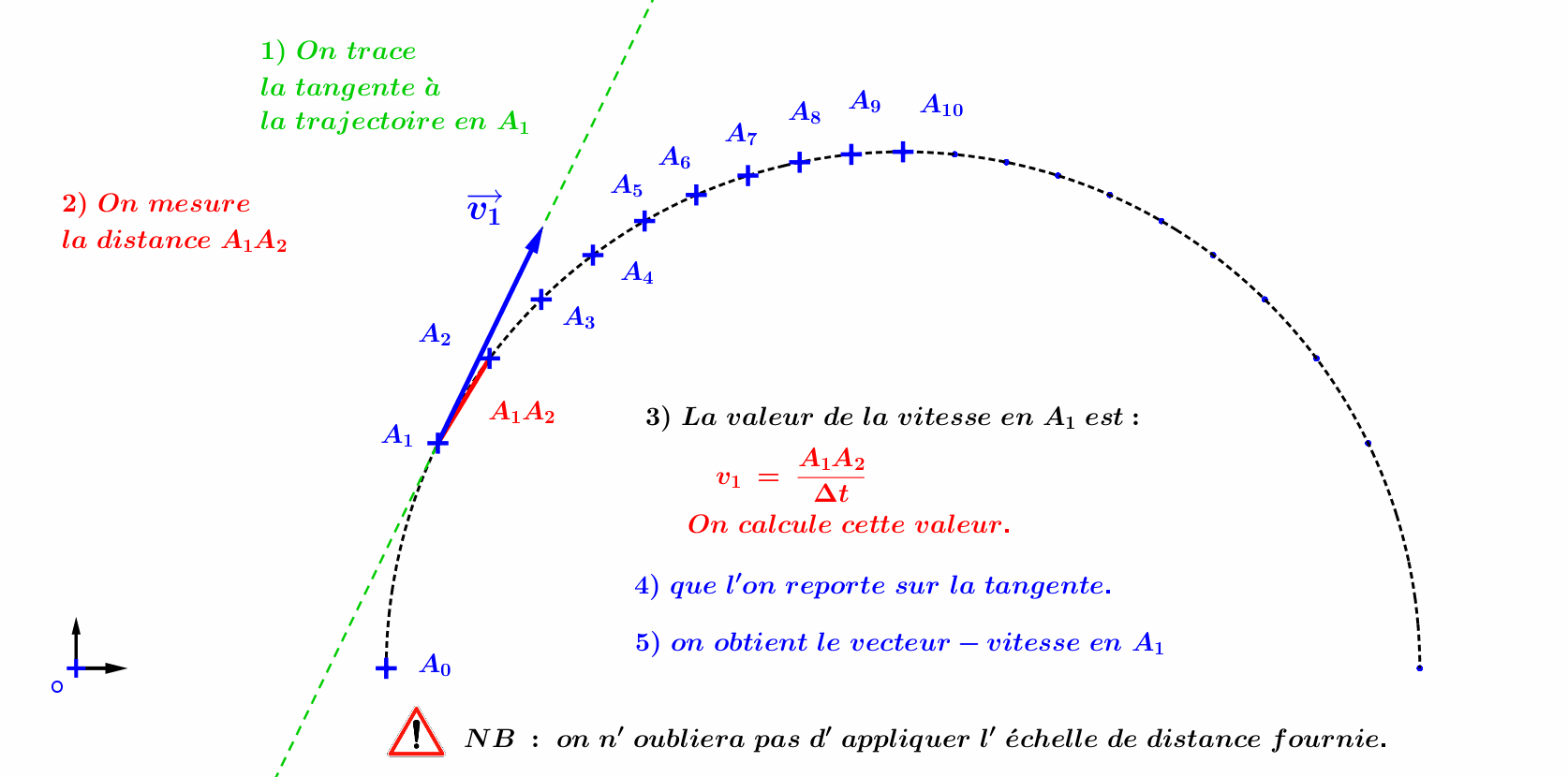
A02 : Tracé du vecteur accélération :
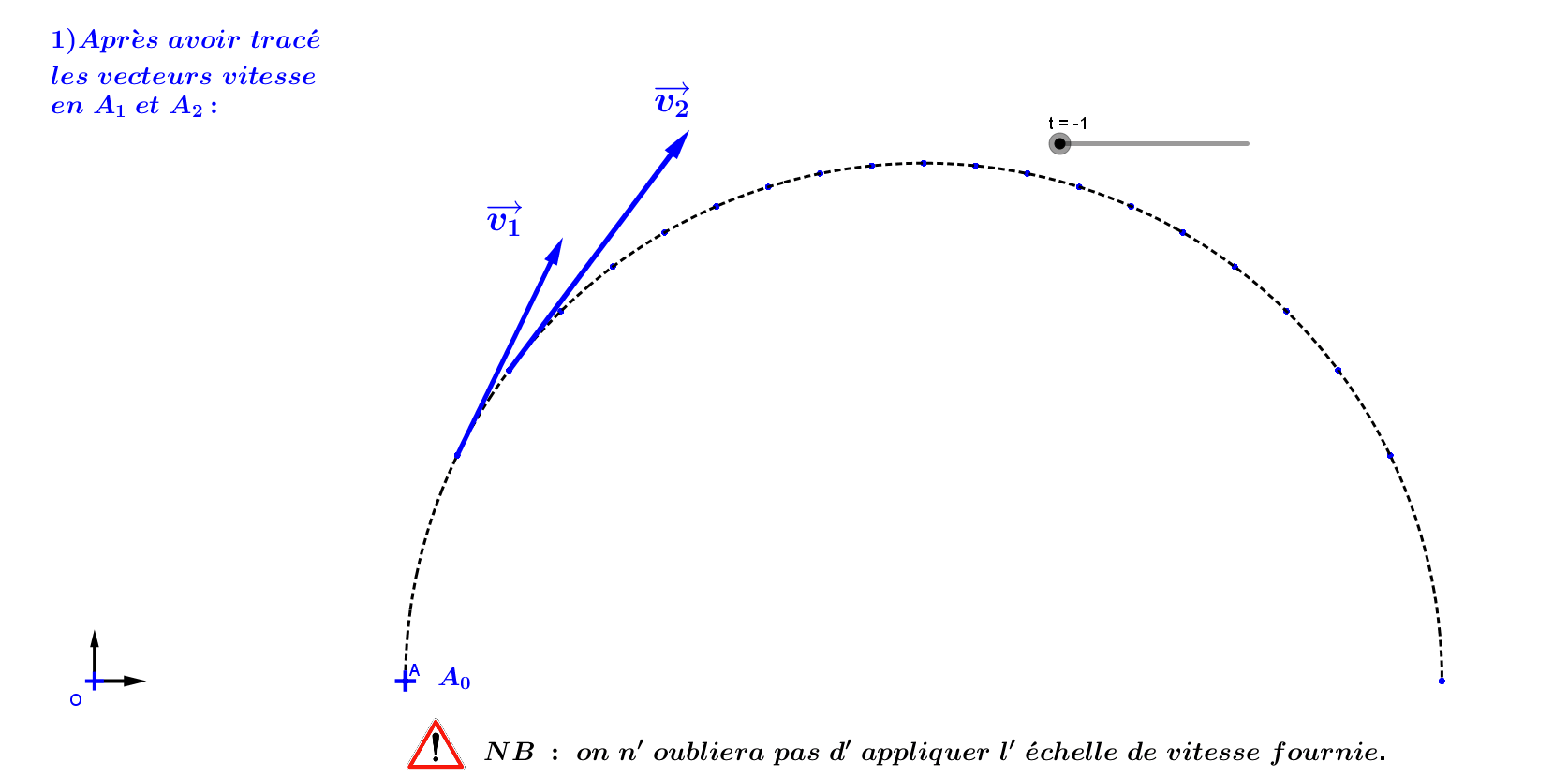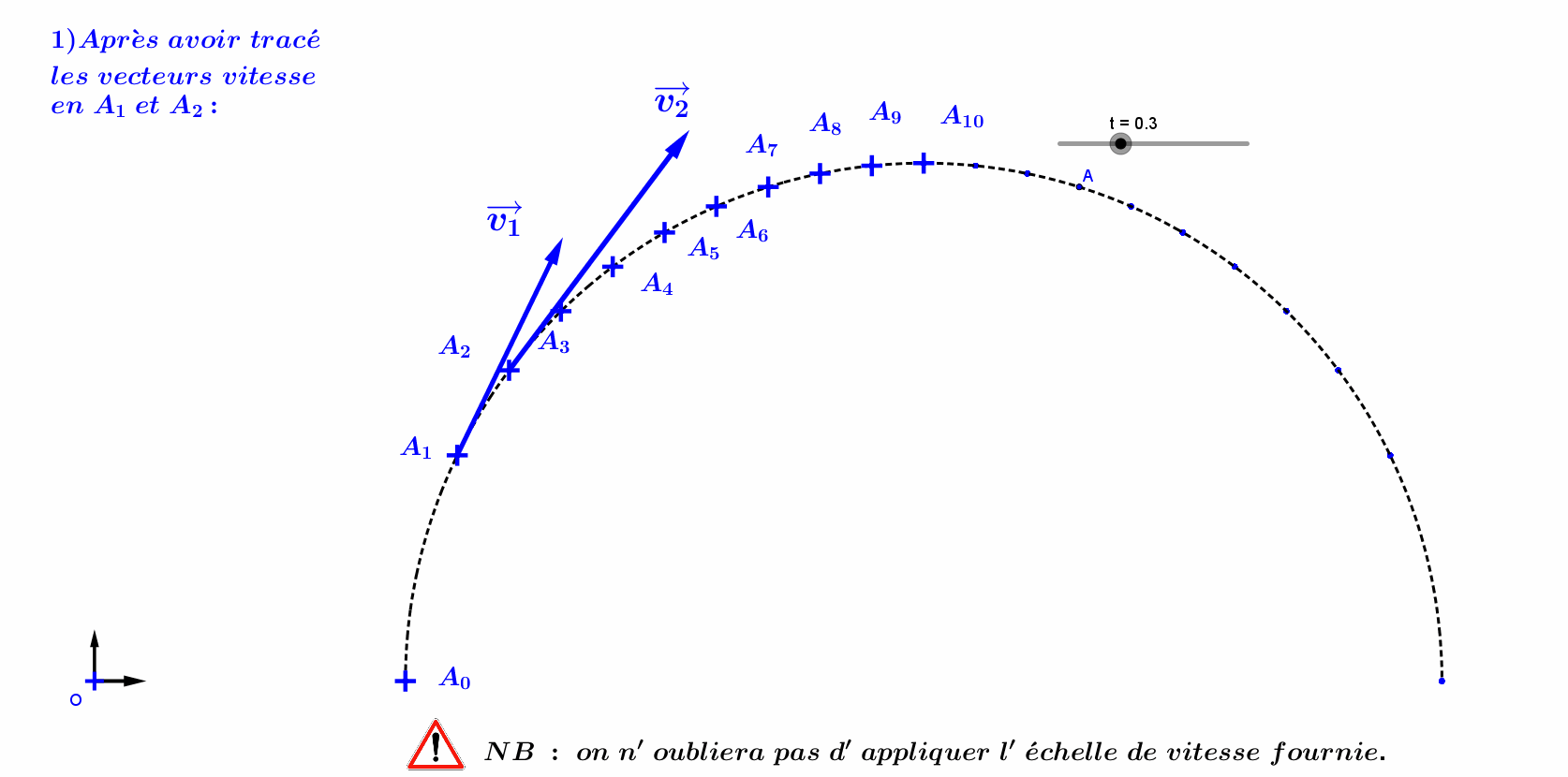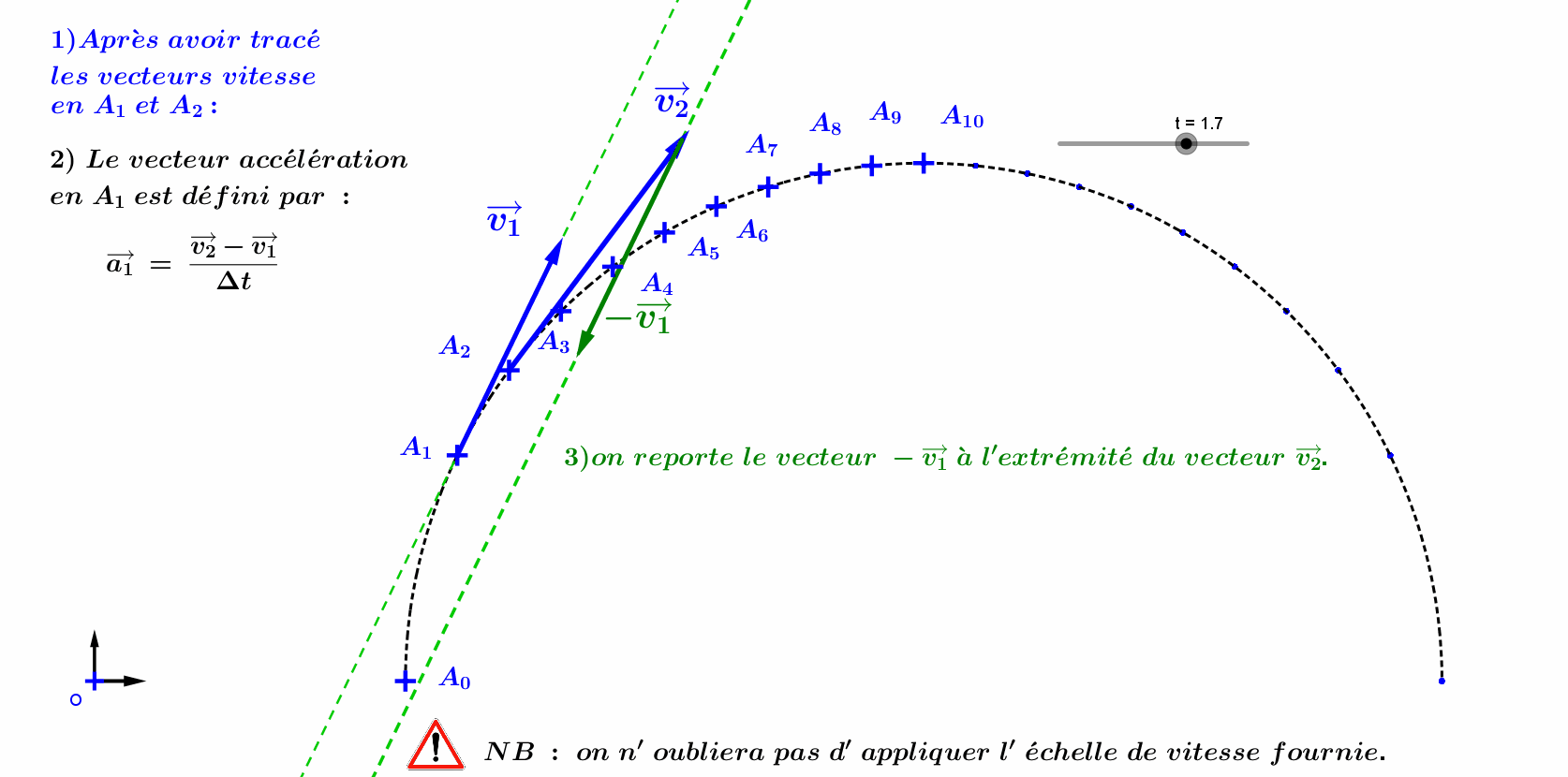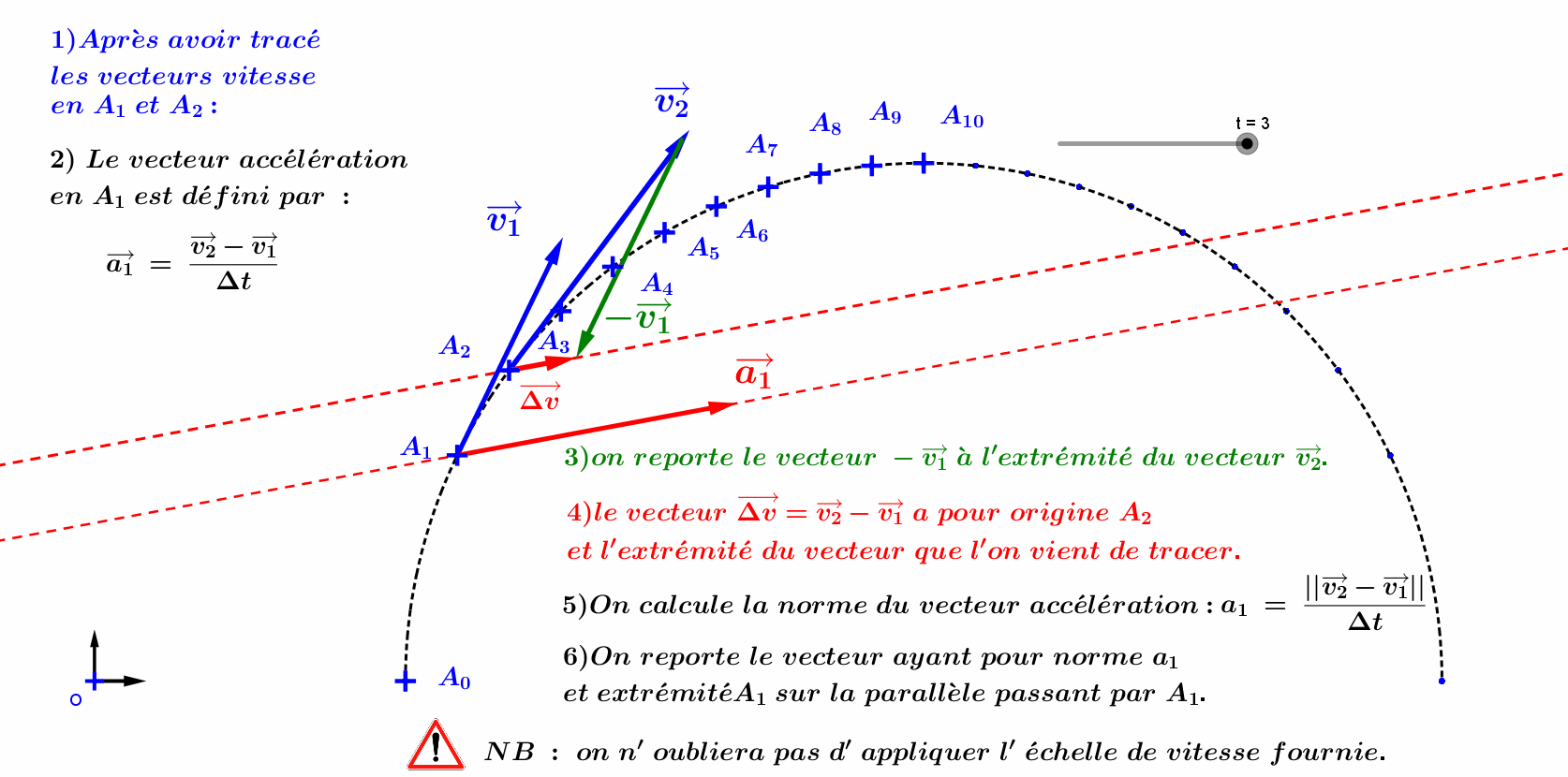
A1 : Etude du mouvement d'une voiture.
Afin de mesurer les émissions polluantes des véhicules, on les soumet à différents cycles, accélérations, décélérations et paliers de vitesse de valeurs constantes.
Un des tests appelé "urbain" consiste à faire passer une voiture de 0 à 50 km/h en 26 s.
Comment définir les vecteurs vitesse et accélération ?
|
|
|
Doc4 : Pour un point M en mouvement rectiligne sur un axe (Ox):
|
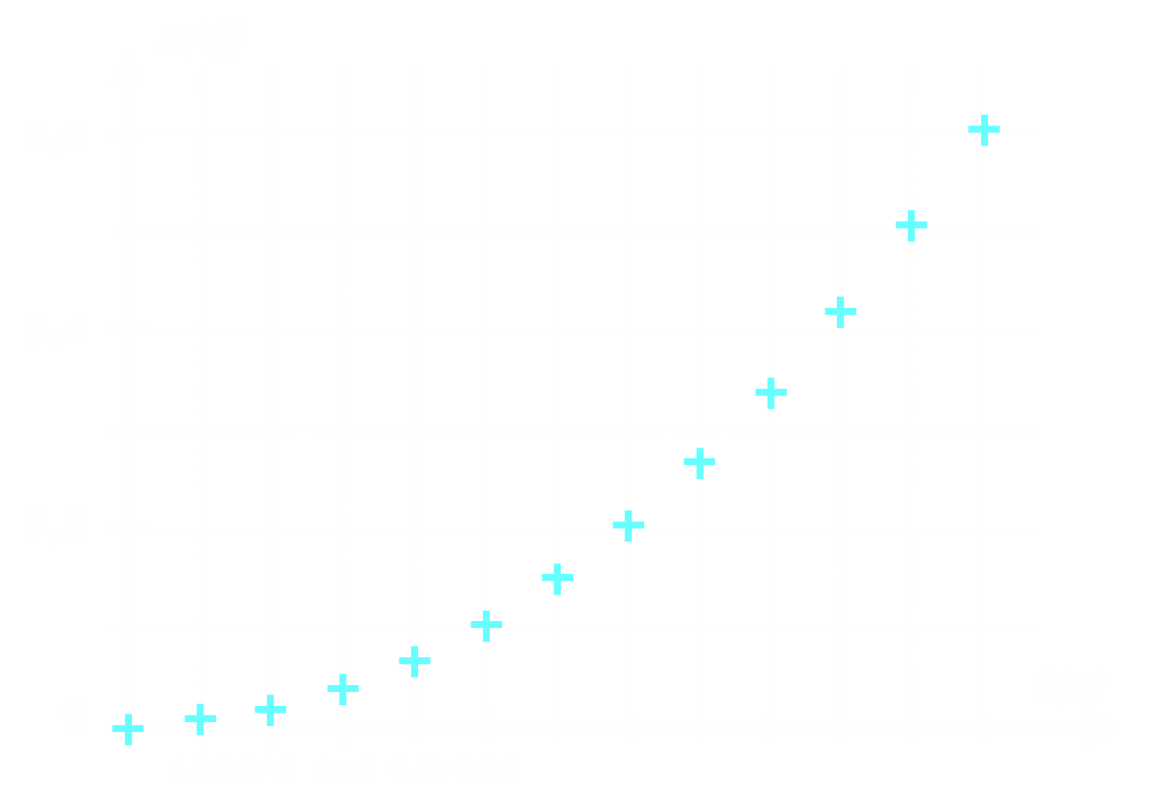
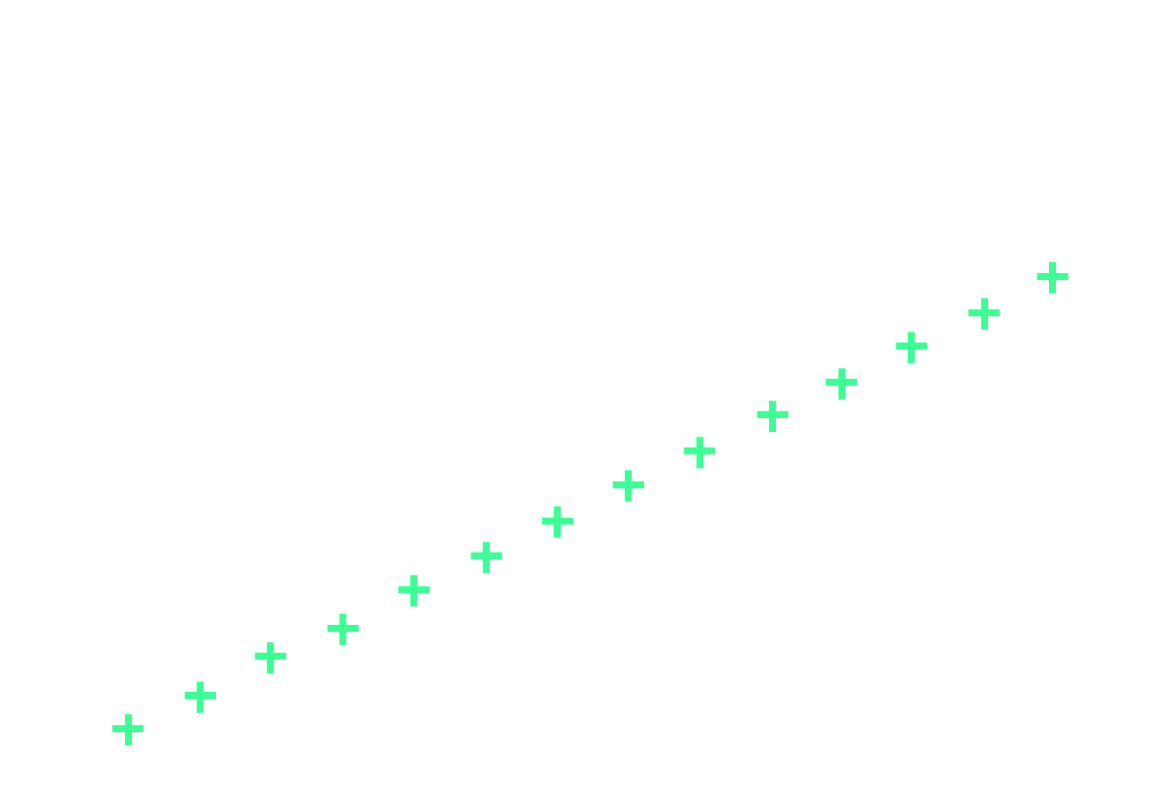
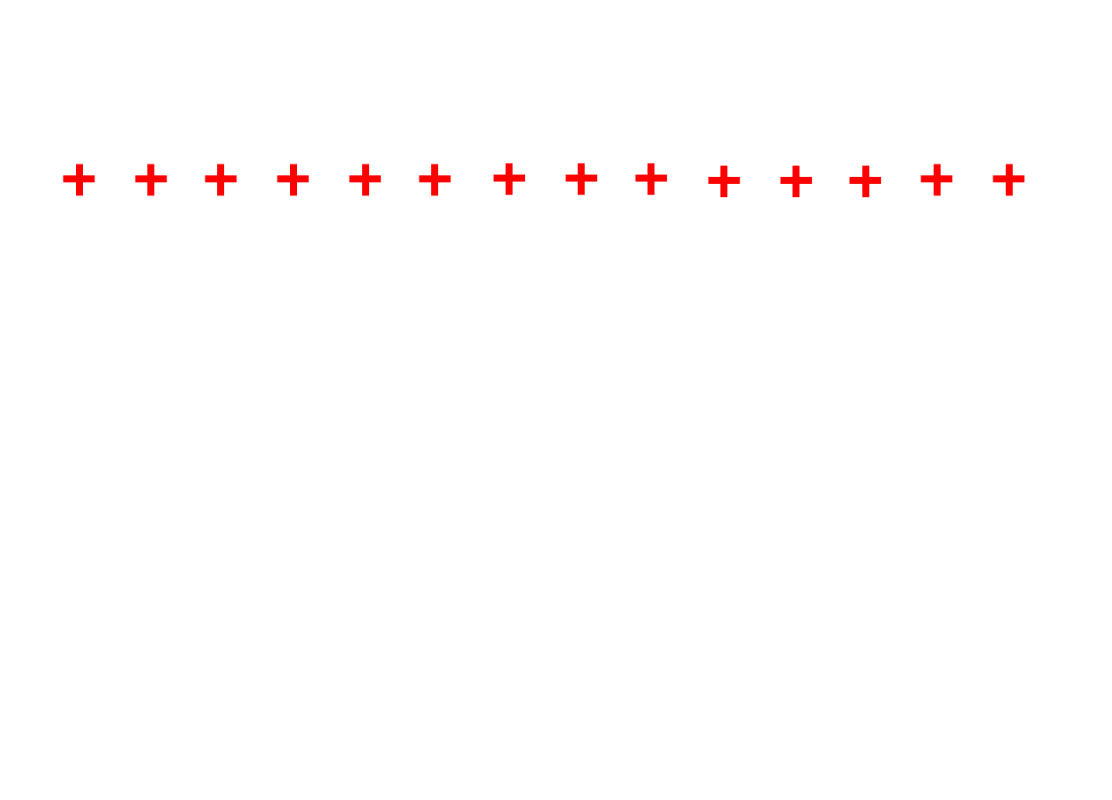
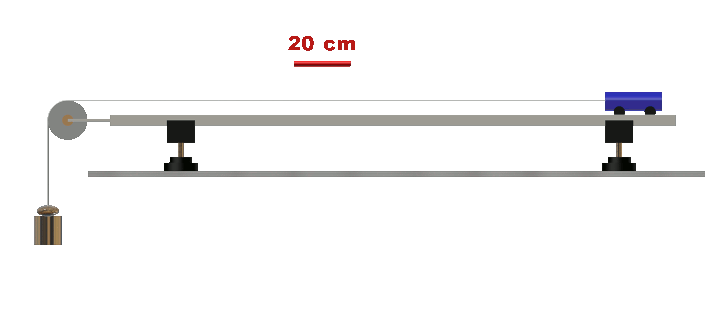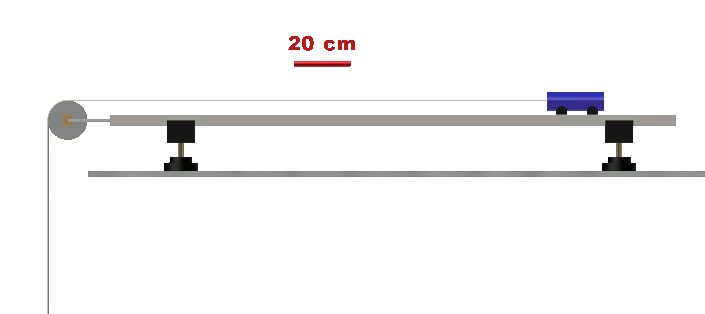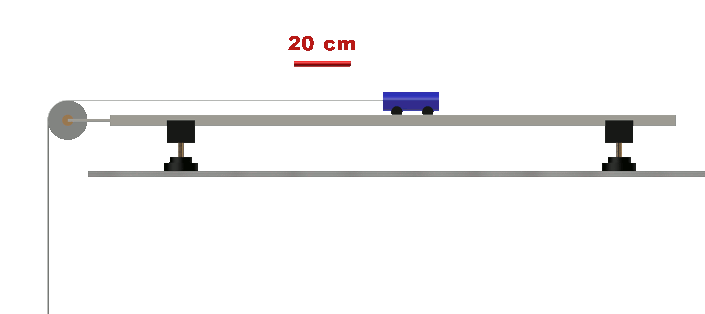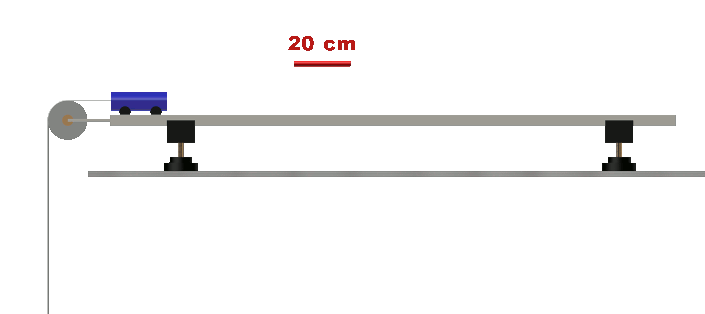
• Proposer et mettre en œuvre un protocole permettant de tracer l’évolution de l’abscisse x d’un point M d’une maquette de voiture accélérée de façon constante en fonction du temps ?
(fichier vidéo : 1-250g_0-70N.mp4 ou Chariotplan.gif fournis)
•Utiliser les outils de modélisation d’un logiciel tableur grapheur (Regressi ou Excel, Regressi étant recommandé car au cours de l’année on ne pourra pas toujours utiliser Excel) pour déterminer l’équation
x = f(t). L’allure de la courbe est-elle similaire à la courbe du doc2 ?
• En déduire les équations vx(t) = g(t) et ax(t) = h(t).
• Quelle est la valeur de l’accélération, supposée constante, d’une voiture lors d’un test correspondant au cycle urbain ?
• Comment définir la vitesse et l’accélération ? Avec la trajectoire obtenue sur les pointages que l’on aura préalablement imprimés, tracer les vecteurs vitesse et accélération (méthode graphique) de la voiture. (à faire chez soi)
A2 : Se comparer aux plus grands.
|
Doc 1 : Chronophotographie.
|
|
Doc 2 : Protocole. • À deux, se rendre sur une piste dégagée pour réaliser la chronophotographie. • Identifier un objet ou une distance de référence, qui sera visible sur la chronophotographie, et la mesurer. • Se positionner à une dizaine de mètres, perpendiculairement à la piste de course. • Lancer l’application Motion Shot et garder la position fixe. • Au top départ, le coureur se lance dans le champ d’acquisition de l’appareil. • Attendre que le coureur parcoure l’intégralité du champ et arrêter l’enregistrement. • Ajuster la chronophotographie en choisissant l’image de départ et l’image de fin. Noter les dates tf? et ti? correspondant respectivement aux dates de fin et de début de la chronophotographie. • Enregistrer l’image choisie et l’exporter sur un ordinateur pour son exploitation. On approxime les vitesses vi à chaque point aux vitesses moyennes entre les instants ti? et ti+1?, il faut alors calculer les grandeurs vxi et vyi en utilisant les relations : $ v_{xi}\left ( t_{i} \right ) = \dfrac { x(t_{i+1}) - x(t_{i})}{\Delta t} $
|
• Déterminer l’écart de temps Δt correspondant à $ \Delta t = \dfrac {t_{f} - t_{0}}{N}$, puis calculer automatiquement les trois grandeurs précédemment évoquées.
• Visualiser l’évolution de la vitesse du coureur v(t) en fonction du temps t et évaluer son accélération moyenne a correspondant au rapport entre la variation de vitesse et la durée de la variation.
• Comparer la vitesse maximale vmax? obtenue avec les vitesses des grands champions du 100 m sur Internet.
A3 : Mouvement de la Terre sur son orbite.
|
|
Travail à effectuer et à remettre sous la forme d'un compte-rendu clair.
• A l'aide d'un logiciel de pointage vidéo, et de la simulation "espace.avi" (ou en chargeant le fichier gif ci-dessus) :
- Repérer les positions de la Terre au cours de son mouvement.
- Déterminer les coordonnées du vecteur vitesse.
- Déterminer les coordonnées du vecteur accélération.
- Tracer le vecteur vitesse. Commenter.
- Tracer le vecteur accélération. Commenter.
- Déterminer la vitesse moyenne et l'incertitude associée.
-Déterminer l'accélération et l'incertitude associée.
- Qualifier le mouvement de la Terre autour du Soleil.
• Sachant que la valeur moyenne de l'accélération est de la forme $ a= k \times \dfrac {v^{2}}{R} $, déterminer la valeur de k.
• Donner l'expression de la force exercée par le Soleil sur la Terre, et donner sa valeur F. Effectuer le rapport de la force à l'accélération. Quelle est la valeur ainsi obtenue ?
A4 : London Eye.
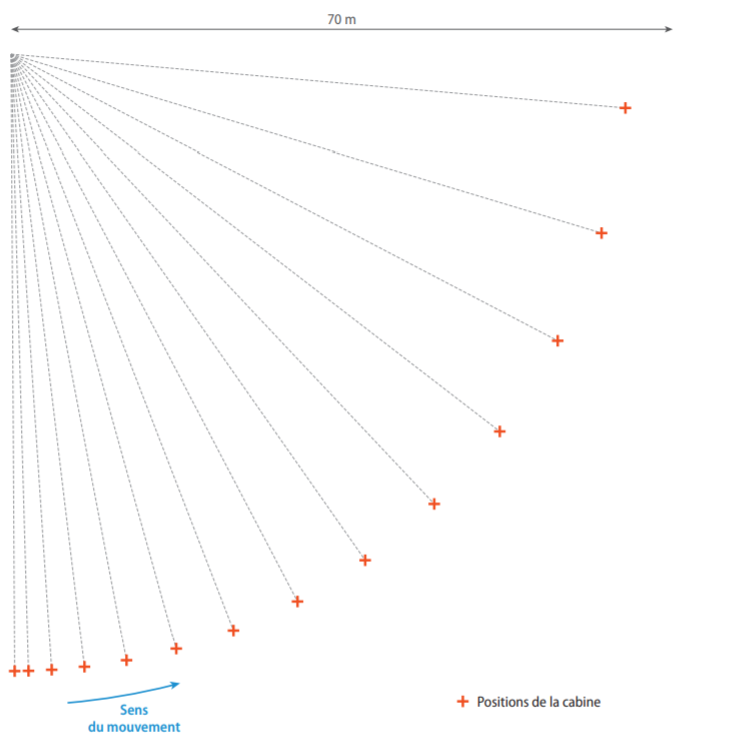
| Le London Eye, grande roue de Londres, a un diamètre R = 130 m. La vitesse maximale atteinte par les cabines est de 0,9 km/h. On étudie l'enregistrement des positions d'un cabine (représentée par son centre d'inertie M) à partir de sa position de départ (en bas). Les positions sont relevées à intervalle de temps régulier Δt = 40 s. |  |
L'objectif est ici de tracer les vecteur vitesse et accélération au démarrage de la cabine.
Echelles :
Pour les vitesses, 1 cm papier correspond à 0,1m/s.
Pour les accélérations, 1 cm papier représente 2,5.10-4 m/s2.
|
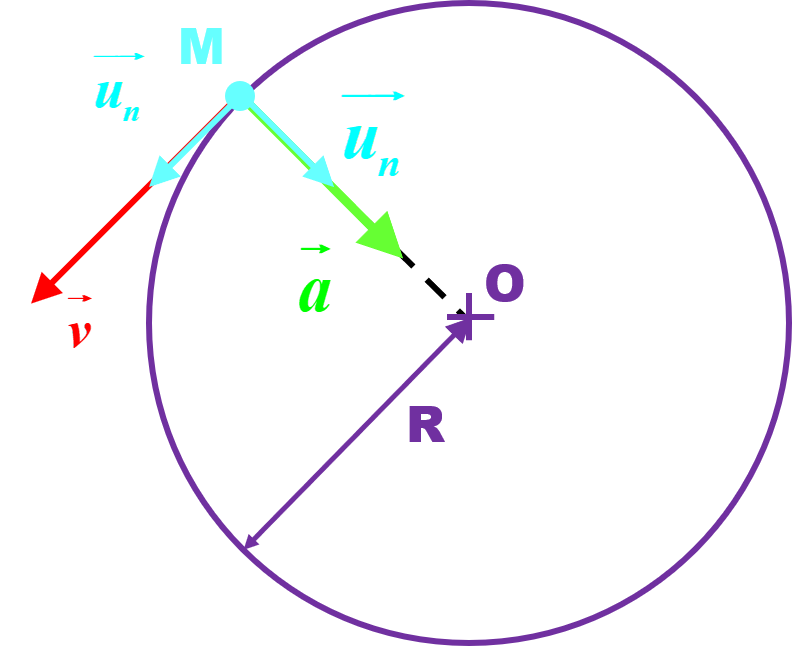
Le repère de Frenet !
|
1. Numéroter les points de M1 à M14 et tracer la trajectoire du point M.
2. Tracer les vecteurs vitesse $\overrightarrow {v_{10}}$ ,$\overrightarrow {v_{11}}$ et $\overrightarrow {v_{12}}$ aux points M10, M11 et M12. On détaillera les calculs.
3. Le vecteur vitesse est-il constant au cours du mouvement ? Commenter alors le mouvement de la cabine.
4. Tracer le vecteur vitesse ${\overrightarrow {\Delta v_{10}}}$ au point M10.
5. Déterminer la norme du vecteur ${\overrightarrow {a_{10}}}$ au point M10. On détaillera les calculs.
6. Au point M10, tracer le repère de Frenet. Projeter le vecteur $\overrightarrow {a_{10}}$ sur ce repère et en déduire les valeurs des composantes normale et tangentielle de l'accélération. En déduire la nature du mouvement.
7. Reprendre le travail avec un logiciel de pointage et retrouver les conclusions précédentes.
Exercices : 10, 11, 12, 13, 15, 17, 19, 23, 24, 26, 28, 29, 30, 31, 33, 35, 40, 43, 46 P 254 à 265.
COURS
C1 : Les vecteurs du mouvement.
C11 : Le vecteur position.
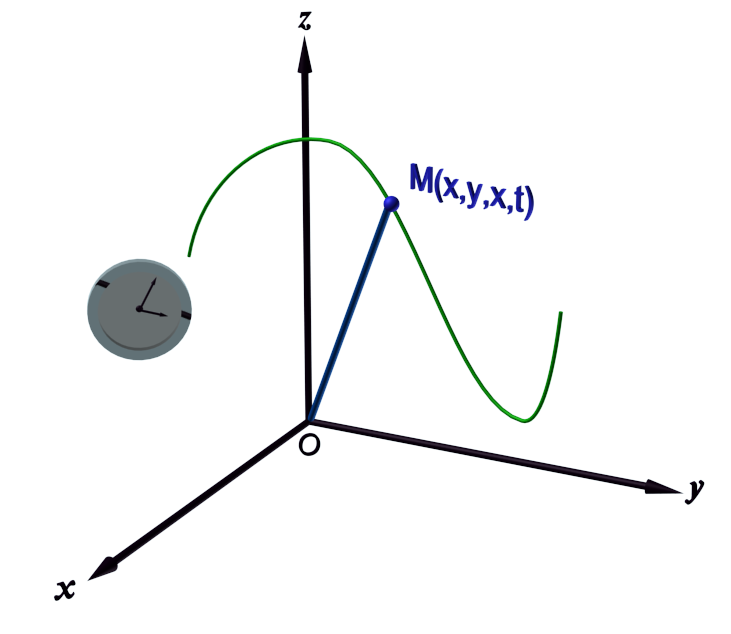 |
Pour étudier le mouvement d'un mobile M, on détermine à chaque instant t les coordonnées x(t), y(t) et z(t) de ce mobile. $ \overrightarrow {OM(t)} = |
C12 : Le vecteur vitesse.
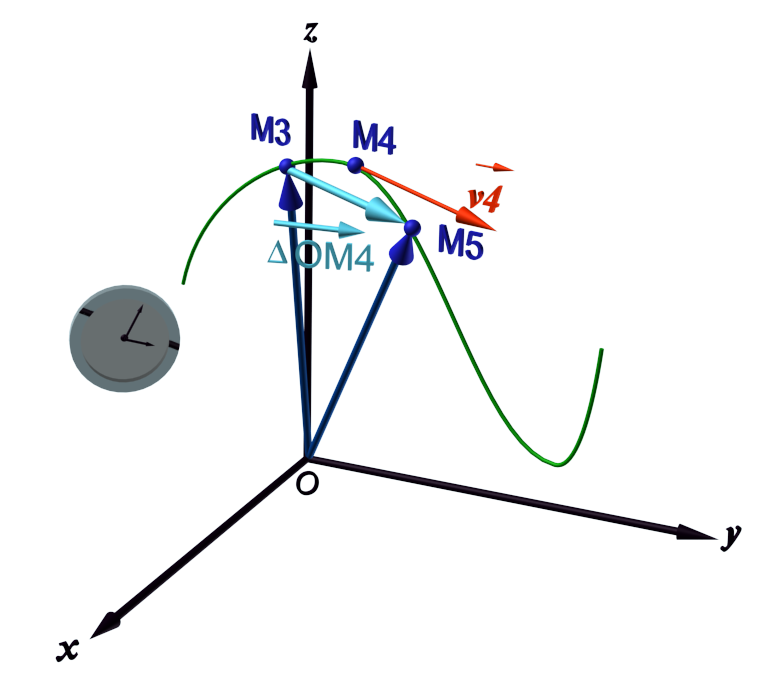 |
Le vecteur vitesse décrit l'évolution de la position au cours du temps. Il se calcule à un instant donné ti à partir du vecteur $\Delta \overrightarrow {OM} (t_i) = \overrightarrow {OM} (t_{i+1}) -\overrightarrow {OM} (t_{i+1})$ représentant la variation du vecteur position entre les instants au moment donné et suivant : $\bf {\vec v (t_i) = \frac {\overrightarrow {OM}(t_{i+1} - \overrightarrow {OM}(t_{i})}{\Delta t } = \frac {\Delta \overrightarrow {OM}(t_{i})}{\Delta t}} $
Lorsqu'on fait tendre Δt vers 0, ce vecteur tend vers le vecteur dérivé du vecteur position.
$\bf{\vec v (t) = \frac {d \overrightarrow {OM}(t)}{dt}}$
Caractéristiques :
|
C13 : Le vecteur accélération.
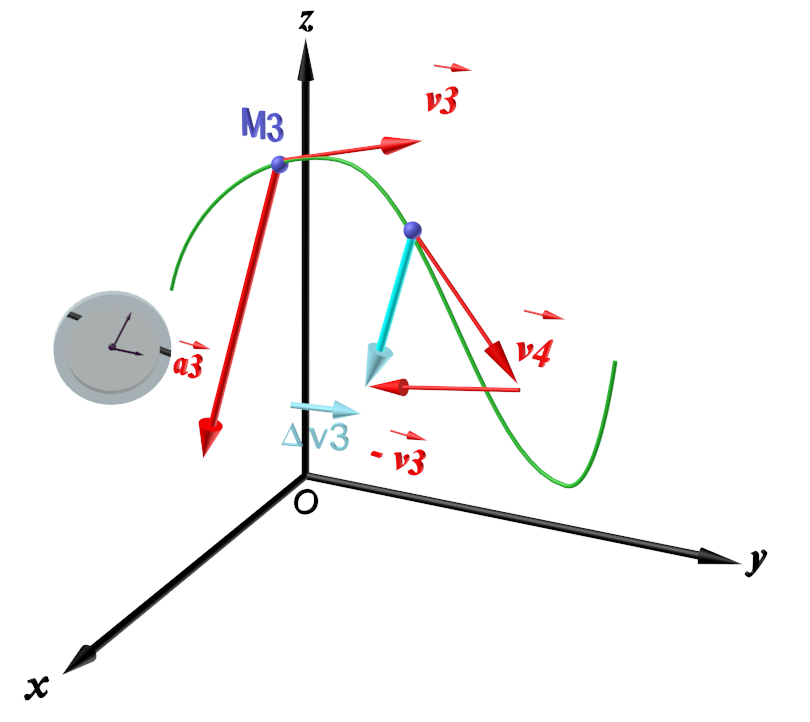 |
Le vecteur accélération décrit l'évolution de la vitesse au cours du temps. Il se calcule à un instant donné ti à partir du vecteur $\Delta \overrightarrow {v} (t_i) = \overrightarrow {v} (t_{i+1}) -\overrightarrow {v} (t_{i})$ représentant la variation du vecteur position entre les instants précédent et suivant : $\bf {\vec a (t_i) = \frac {\overrightarrow {v}(t_{i+1} - \overrightarrow {v}(t_{i})}{\Delta t } = \frac {\Delta \overrightarrow {v}(t_{i})}{\Delta t}} $
Lorsqu'on fait tendre Δt vers 0, ce vecteur tend vers le vecteur accélération du vecteur vitesse. $\bf{\vec a (t) = \frac {d \overrightarrow {v}(t)}{dt}}$.
Il est exprimé en m.s-2. |
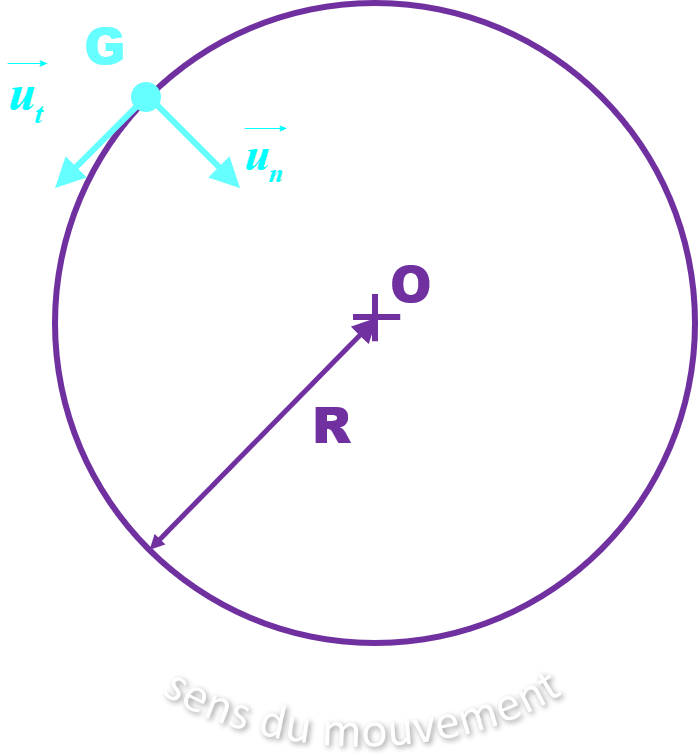
C2 : La base de Frenet.
C21 : Définition.
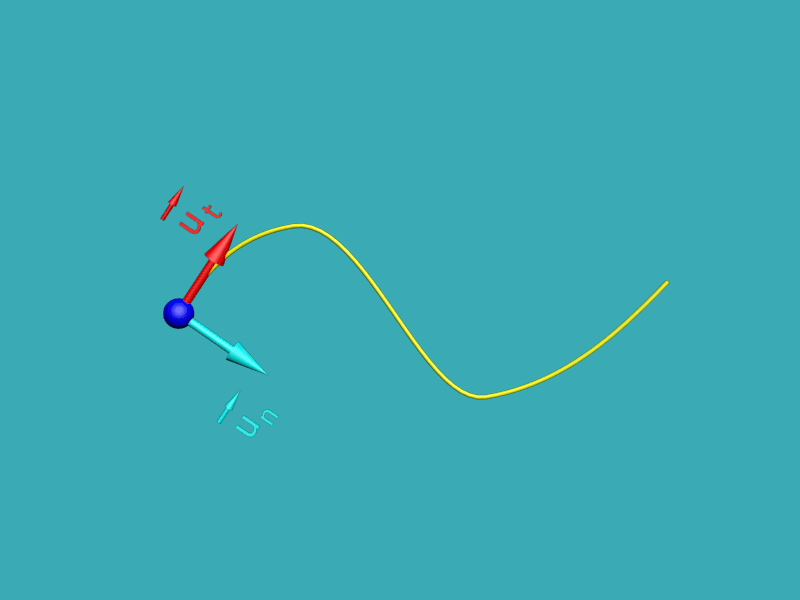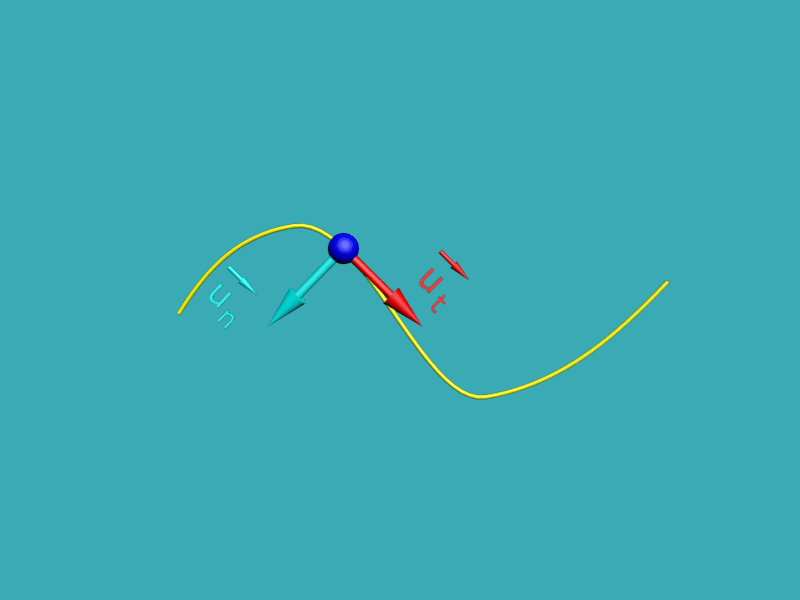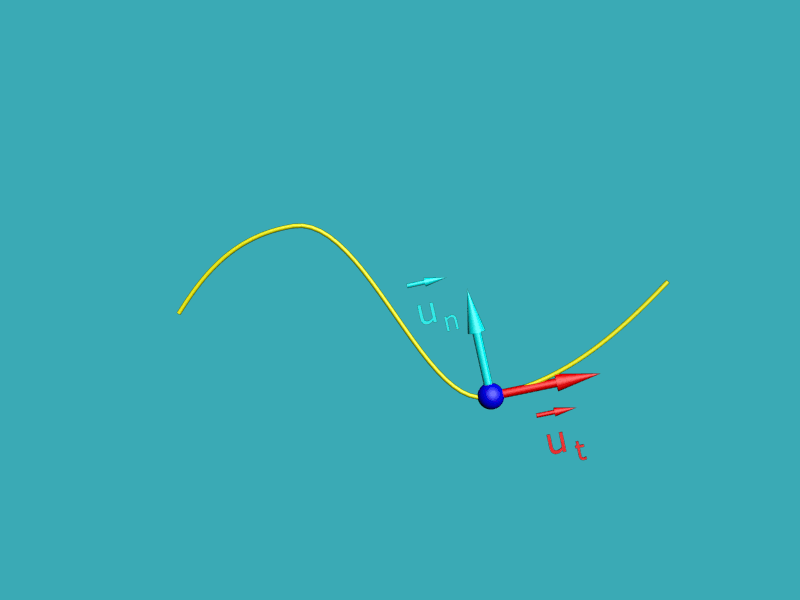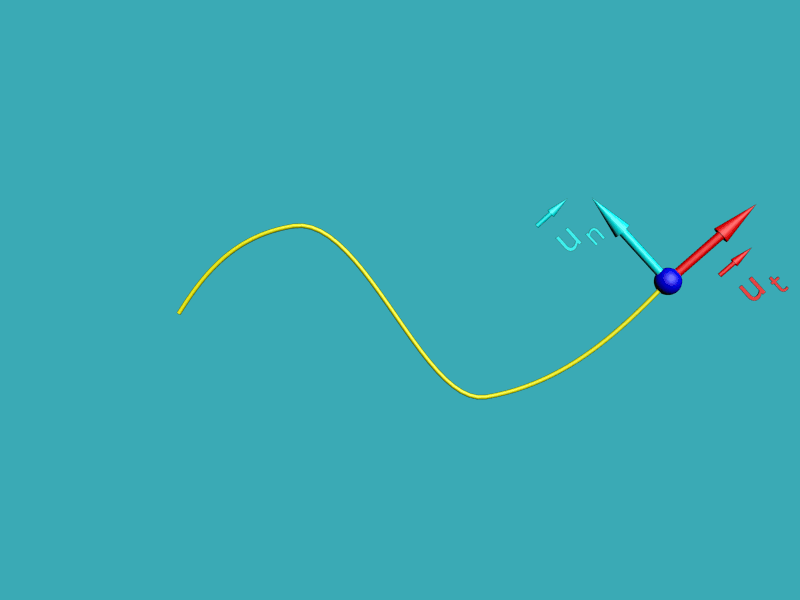 |
La base de Frenet est définie à partir de deux vecteurs unitaires orthogonaux $\overrightarrow {u_{t}}$ et $\overrightarrow {u_{n}}$ En chaque point de la trajectoire : $\overrightarrow {u_{t}}$ est tangent à la trajectoire dans le sens du mouvement, $\overrightarrow {u_{t}}$ est orthogonal à $\overrightarrow {u_{n}}$ et centripète.
Cette base est locale car elle dépend du point de la trajectoire auquel on s'intéresse. |
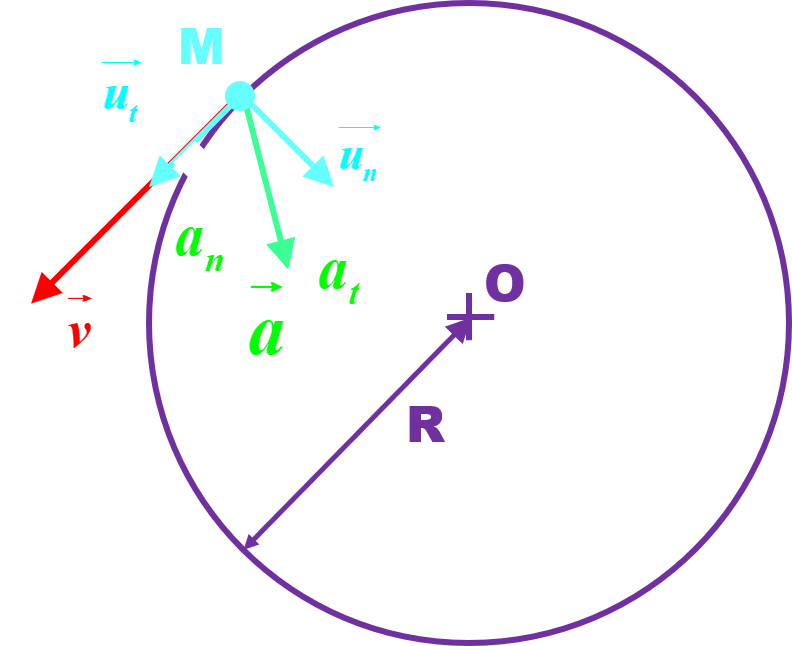
C22 : Pour les mouvements circulaires.
|
Les vecteurs vitesse et accélération se composent ainsi : • Le vecteur vitesse $\vec v(t) $ étant tangent à la trajectoire, il n'a pas de composante selon $\overrightarrow {u_{n}}$ :
$ \vec a = a_{t} \overrightarrow {u_t} + a_n\overrightarrow {u_n} =
an : accélération normale en m.s-2. at : accélération tangentielle en m.s-2. R : rayon de la trajectoire, en m.
|
C3 : Mouvements particuliers.
C31 : Mouvements rectilignes.
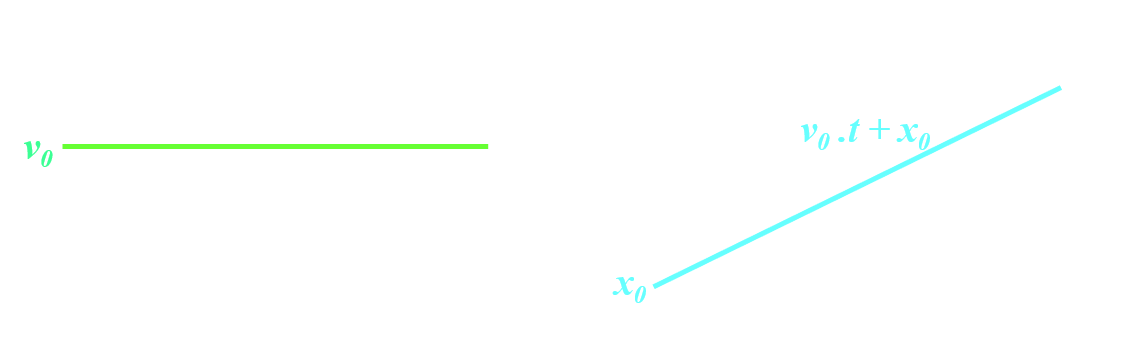
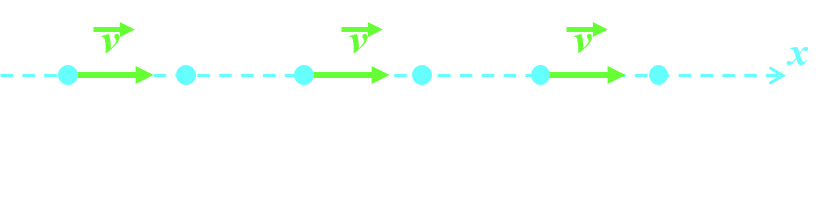
C311 : Mouvement rectiligne uniforme.
|
La trajectoire du point est une droite et sa vitesse est constante : v(t) = v0 . Son accélération est nulle : a(t) = 0. |
 |
|
La vitesse ne varie pas au cours du temps : v(t) = v0 NB : l'expression de v(t) est obtenue en dérivant celle de la position.
$v(t) = \dfrac {dx(t)}{dt}$ |
La position est une fonction affine du temps : x(t) = v0. t + x0 NB : l'expression de x(t) est obtenue en "intégrant" celle de la vitesse.
|
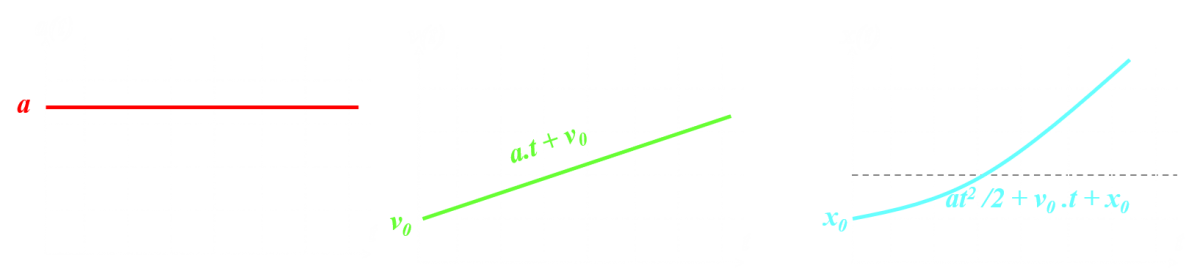
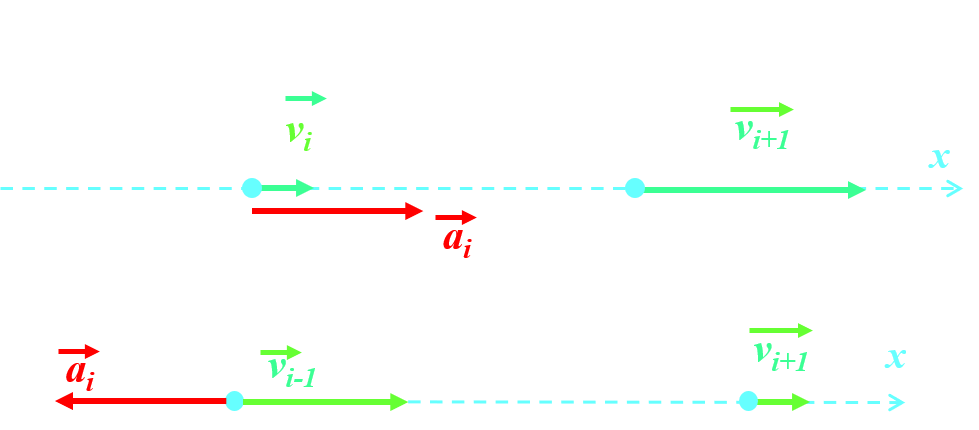
C311 : Mouvement rectiligne uniformément varié.
|
La trajectoire du point est une droite et sa vitesse est une fonction affine du temps : v(t) = v0 . Son accélération est nulle : a(t) = a. |
 |
|
L'accélération est une fonction constante du temps. a(t) = a NB : l'expression de a(t) est obtenue en "dérivant" celle de la vitesse : $a(t) = \dfrac {dv(t)}{dt}$ |
La vitesse varie linérairement au cours du temps : v(t) = a.t + v0 NB : l'expression de v(t) est obtenue en "dérivant" celle de la position : $v(t) = \dfrac {dx(t)}{dt}$ |
La position est une fonction du second degré du temps : x(t) = |
C33 : Mouvement circulaire uniforme.
|
La trajectoire est circulaire et la vitesse constante, ainsi, $ \dfrac {dv}{dt} = 0 $ et dans la base de Frenet :
$ \vec a = a_n\overrightarrow {u_n} = |
Ajouter un commentaire